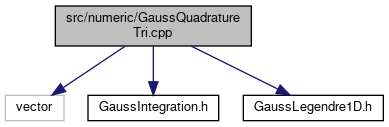
Go to the source code of this file.
Functions | |
| static std::vector< IntPt * > | GQTGL (40, nullptr) |
| IntPt * | getGQTPts (int order, bool forceTensorRule) |
| int | getNGQTPts (int order, bool forceTensorRule) |
Variables | |
| IntPt | GQT1 [1] |
| IntPt | GQT2 [3] |
| IntPt | GQT3 [4] |
| IntPt | GQT4 [6] |
| IntPt | GQT5 [7] |
| IntPt | GQT6 [12] |
| IntPt | GQT7 [13] |
| IntPt | GQT8 [16] |
| IntPt * | GQT [9] = {GQT1, GQT1, GQT2, GQT3, GQT4, GQT5, GQT6, GQT7, GQT8} |
| int | GQTnPt [9] = {1, 1, 3, 4, 6, 7, 12, 13, 16} |
| IntPt | triP1Solin [1] |
| IntPt | triP2Solin [3] |
| IntPt | triP3Solin [4] |
| IntPt | triP4Solin [6] |
| IntPt | triP5Solin [7] |
| IntPt | triP6Solin [12] |
| IntPt | triP7Solin [13] |
| IntPt | triP8Solin [16] |
| IntPt | triP9Solin [19] |
| IntPt | triP10Solin [25] |
| IntPt | triP11Solin [27] |
| IntPt | triP12Solin [33] |
| IntPt | triP13Solin [37] |
| IntPt | triP14Solin [42] |
| IntPt | triP15Solin [48] |
| IntPt | triP16Solin [52] |
| IntPt | triP17Solin [61] |
| IntPt | triP18Solin [70] |
| IntPt | triP19Solin [73] |
| IntPt | triP20Solin [79] |
| static IntPt * | GQTSolin [21] |
| static int | GQTnPtSolin [21] |
Function Documentation
◆ getGQTPts()
| IntPt* getGQTPts | ( | int | order, |
| bool | forceTensorRule | ||
| ) |
Definition at line 889 of file GaussQuadratureTri.cpp.
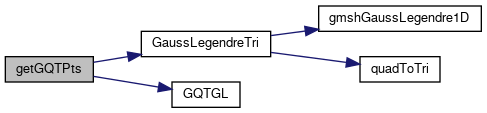
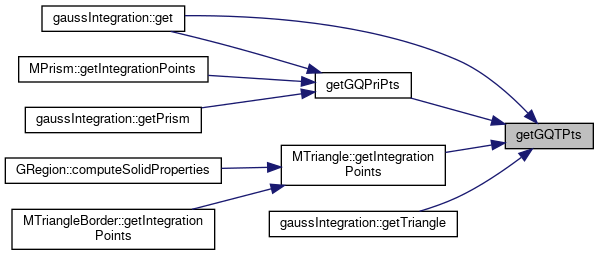
Referenced by gaussIntegration::get(), getGQPriPts(), MTriangle::getIntegrationPoints(), and gaussIntegration::getTriangle().
◆ getNGQTPts()
| int getNGQTPts | ( | int | order, |
| bool | forceTensorRule | ||
| ) |
Definition at line 904 of file GaussQuadratureTri.cpp.
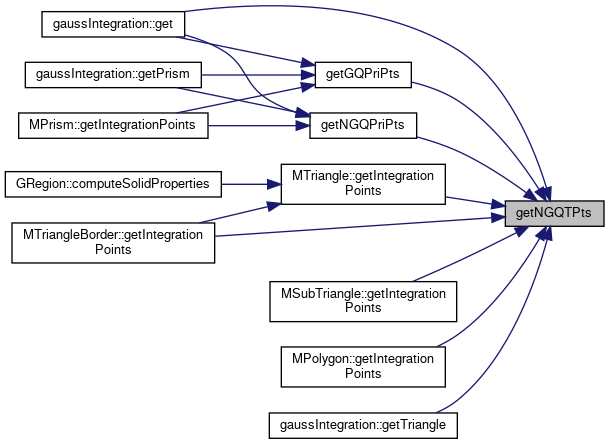
Referenced by gaussIntegration::get(), getGQPriPts(), MTriangle::getIntegrationPoints(), MSubTriangle::getIntegrationPoints(), MPolygon::getIntegrationPoints(), MTriangleBorder::getIntegrationPoints(), getNGQPriPts(), and gaussIntegration::getTriangle().
◆ GQTGL()
|
static |
Variable Documentation
◆ GQT
Definition at line 89 of file GaussQuadratureTri.cpp.
◆ GQT1
| IntPt GQT1[1] |
Definition at line 10 of file GaussQuadratureTri.cpp.
◆ GQT2
| IntPt GQT2[3] |
Definition at line 12 of file GaussQuadratureTri.cpp.
◆ GQT3
| IntPt GQT3[4] |
Definition at line 17 of file GaussQuadratureTri.cpp.
◆ GQT4
| IntPt GQT4[6] |
Definition at line 23 of file GaussQuadratureTri.cpp.
◆ GQT5
| IntPt GQT5[7] |
Definition at line 31 of file GaussQuadratureTri.cpp.
◆ GQT6
| IntPt GQT6[12] |
Definition at line 40 of file GaussQuadratureTri.cpp.
◆ GQT7
| IntPt GQT7[13] |
Definition at line 54 of file GaussQuadratureTri.cpp.
◆ GQT8
| IntPt GQT8[16] |
Definition at line 71 of file GaussQuadratureTri.cpp.
◆ GQTnPt
| int GQTnPt[9] = {1, 1, 3, 4, 6, 7, 12, 13, 16} |
Definition at line 90 of file GaussQuadratureTri.cpp.
◆ GQTnPtSolin
|
static |
Definition at line 885 of file GaussQuadratureTri.cpp.
Referenced by getNGQTPts().
◆ GQTSolin
|
static |
◆ triP10Solin
| IntPt triP10Solin[25] |
Quadrature rule for an interpolation of order 10 on the triangle
Definition at line 249 of file GaussQuadratureTri.cpp.
◆ triP11Solin
| IntPt triP11Solin[27] |
Quadrature rule for an interpolation of order 11 on the triangle
Definition at line 282 of file GaussQuadratureTri.cpp.
◆ triP12Solin
| IntPt triP12Solin[33] |
Quadrature rule for an interpolation of order 12 on the triangle
Definition at line 317 of file GaussQuadratureTri.cpp.
◆ triP13Solin
| IntPt triP13Solin[37] |
Quadrature rule for an interpolation of order 13 on the triangle
Definition at line 358 of file GaussQuadratureTri.cpp.
◆ triP14Solin
| IntPt triP14Solin[42] |
Quadrature rule for an interpolation of order 14 on the triangle
Definition at line 403 of file GaussQuadratureTri.cpp.
◆ triP15Solin
| IntPt triP15Solin[48] |
Quadrature rule for an interpolation of order 15 on the triangle
Definition at line 453 of file GaussQuadratureTri.cpp.
◆ triP16Solin
| IntPt triP16Solin[52] |
Quadrature rule for an interpolation of order 16 on the triangle
Definition at line 509 of file GaussQuadratureTri.cpp.
◆ triP17Solin
| IntPt triP17Solin[61] |
Quadrature rule for an interpolation of order 17 on the triangle
Definition at line 569 of file GaussQuadratureTri.cpp.
◆ triP18Solin
| IntPt triP18Solin[70] |
Quadrature rule for an interpolation of order 18 on the triangle
Definition at line 638 of file GaussQuadratureTri.cpp.
◆ triP19Solin
| IntPt triP19Solin[73] |
Quadrature rule for an interpolation of order 19 on the triangle
Definition at line 716 of file GaussQuadratureTri.cpp.
◆ triP1Solin
| IntPt triP1Solin[1] |
Quadrature rule for an interpolation of order 1 on the triangle
Definition at line 96 of file GaussQuadratureTri.cpp.
◆ triP20Solin
| IntPt triP20Solin[79] |
Quadrature rule for an interpolation of order 20 on the triangle
Definition at line 797 of file GaussQuadratureTri.cpp.
◆ triP2Solin
| IntPt triP2Solin[3] |
Quadrature rule for an interpolation of order 2 on the triangle
Definition at line 105 of file GaussQuadratureTri.cpp.
◆ triP3Solin
| IntPt triP3Solin[4] |
Quadrature rule for an interpolation of order 3 on the triangle
Definition at line 116 of file GaussQuadratureTri.cpp.
◆ triP4Solin
| IntPt triP4Solin[6] |
Quadrature rule for an interpolation of order 4 on the triangle
Definition at line 128 of file GaussQuadratureTri.cpp.
◆ triP5Solin
| IntPt triP5Solin[7] |
Quadrature rule for an interpolation of order 5 on the triangle
Definition at line 142 of file GaussQuadratureTri.cpp.
◆ triP6Solin
| IntPt triP6Solin[12] |
Quadrature rule for an interpolation of order 6 on the triangle
Definition at line 157 of file GaussQuadratureTri.cpp.
◆ triP7Solin
| IntPt triP7Solin[13] |
Quadrature rule for an interpolation of order 7 on the triangle
Definition at line 177 of file GaussQuadratureTri.cpp.
◆ triP8Solin
| IntPt triP8Solin[16] |
Quadrature rule for an interpolation of order 8 on the triangle
Definition at line 198 of file GaussQuadratureTri.cpp.
◆ triP9Solin
| IntPt triP9Solin[19] |
Quadrature rule for an interpolation of order 9 on the triangle
Definition at line 222 of file GaussQuadratureTri.cpp.

