GaussQuadratureTet.cpp File Reference

#include <vector>
#include "GaussIntegration.h"
#include "GaussLegendre1D.h"

Include dependency graph for GaussQuadratureTet.cpp:

Go to the source code of this file.

Macros
#define	a4   0.5854101966249685
#define	b4   0.138196601125015
#define	a5   0.500000000000000
#define	b5   0.166666666666667
#define	a16   0.00839563235002047
#define	b16   0.0110903447722154
#define	c16   0.7716429020672371
#define	d16   0.0761190326442543
#define	e16   0.1197005277978019
#define	f16   0.0718316452676693
#define	g16   0.4042339134672644
#define	a17   0.0314030927894235
#define	b17   0.0111730972876738
#define	c17   0.00754759872721232
#define	p17   0.7316369079576180
#define	q17   0.0894543640141273
#define	e17   0.1325810999384657
#define	f17   0.0245400397290300
#define	g17   0.4214394310662522
#define	a29   0.0150668817433579
#define	b29   0.00318663904649853
#define	c29   0.00726915640111095
#define	d29   0.00430194599366527
#define	p29   0.8277192480479295
#define	q29   0.0574269173173568
#define	e29   0.0513518841255634
#define	f29   0.4860510285706072
#define	g29   0.2312985436519147
#define	h29   0.2967538129690260
#define	i29   0.6081079894015281
#define	j29   0.0475690988147229

Functions
static std::vector< IntPt * >	GQTetGL (40, nullptr)
IntPt *	getGQTetPts (int order, bool forceTensorRule)
int	getNGQTetPts (int order, bool forceTensorRule)

Variables
IntPt	GQTet1 [1] = {{{.25, .25, .25}, 0.166666666666667}}
IntPt	GQTet2 [4]
IntPt	GQTet3 [5]
IntPt	GQTet4 [16]
IntPt	GQTet5 [17]
IntPt	GQTet6 [29]
IntPt *	GQTet [7] = {GQTet1, GQTet1, GQTet2, GQTet3, GQTet4, GQTet5, GQTet6}
int	GQTetnPt [7] = {1, 1, 4, 5, 16, 17, 29}
IntPt	tetP1Solin [1] = {{{0.25, 0.25, 0.25}, 0.166666666666667}}
IntPt	tetP2Solin [4]
IntPt	tetP3Solin [5]
IntPt	tetP4Solin [11]
IntPt	tetP5Solin [14]
IntPt	tetP6Solin [24]
IntPt	tetP7Solin [31]
IntPt	tetP8Solin [43]
IntPt	tetP9Solin [53]
IntPt	tetP11Solin [126]
IntPt	tetP13Solin [210]
IntPt	tetP15Solin [330]
IntPt	tetP17Solin [495]
IntPt	tetP19Solin [715]
IntPt	tetP21Solin [1001]
static IntPt *	GQTetSolin [22]
static int	GQTetnPtSolin [22]

Macro Definition Documentation

a16

#define a16   0.00839563235002047

Definition at line 20 of file GaussQuadratureTet.cpp.

a17

#define a17   0.0314030927894235

Definition at line 29 of file GaussQuadratureTet.cpp.

a29

#define a29   0.0150668817433579

Definition at line 39 of file GaussQuadratureTet.cpp.

a4

#define a4   0.5854101966249685

Definition at line 12 of file GaussQuadratureTet.cpp.

a5

#define a5   0.500000000000000

Definition at line 16 of file GaussQuadratureTet.cpp.

b16

#define b16   0.0110903447722154

Definition at line 21 of file GaussQuadratureTet.cpp.

b17

#define b17   0.0111730972876738

Definition at line 30 of file GaussQuadratureTet.cpp.

b29

#define b29   0.00318663904649853

Definition at line 40 of file GaussQuadratureTet.cpp.

b4

#define b4   0.138196601125015

Definition at line 13 of file GaussQuadratureTet.cpp.

b5

#define b5   0.166666666666667

Definition at line 17 of file GaussQuadratureTet.cpp.

c16

#define c16   0.7716429020672371

Definition at line 22 of file GaussQuadratureTet.cpp.

c17

#define c17   0.00754759872721232

Definition at line 31 of file GaussQuadratureTet.cpp.

c29

#define c29   0.00726915640111095

Definition at line 41 of file GaussQuadratureTet.cpp.

d16

#define d16   0.0761190326442543

Definition at line 23 of file GaussQuadratureTet.cpp.

d29

#define d29   0.00430194599366527

Definition at line 42 of file GaussQuadratureTet.cpp.

e16

#define e16   0.1197005277978019

Definition at line 24 of file GaussQuadratureTet.cpp.

e17

#define e17   0.1325810999384657

Definition at line 34 of file GaussQuadratureTet.cpp.

e29

#define e29   0.0513518841255634

Definition at line 45 of file GaussQuadratureTet.cpp.

f16

#define f16   0.0718316452676693

Definition at line 25 of file GaussQuadratureTet.cpp.

f17

#define f17   0.0245400397290300

Definition at line 35 of file GaussQuadratureTet.cpp.

f29

#define f29   0.4860510285706072

Definition at line 46 of file GaussQuadratureTet.cpp.

g16

#define g16   0.4042339134672644

Definition at line 26 of file GaussQuadratureTet.cpp.

g17

#define g17   0.4214394310662522

Definition at line 36 of file GaussQuadratureTet.cpp.

g29

#define g29   0.2312985436519147

Definition at line 47 of file GaussQuadratureTet.cpp.

h29

#define h29   0.2967538129690260

Definition at line 48 of file GaussQuadratureTet.cpp.

i29

#define i29   0.6081079894015281

Definition at line 49 of file GaussQuadratureTet.cpp.

j29

#define j29   0.0475690988147229

Definition at line 50 of file GaussQuadratureTet.cpp.

p17

#define p17   0.7316369079576180

Definition at line 32 of file GaussQuadratureTet.cpp.

p29

#define p29   0.8277192480479295

Definition at line 43 of file GaussQuadratureTet.cpp.

q17

#define q17   0.0894543640141273

Definition at line 33 of file GaussQuadratureTet.cpp.

q29

#define q29   0.0574269173173568

Definition at line 44 of file GaussQuadratureTet.cpp.

Function Documentation

getGQTetPts()

IntPt* getGQTetPts	(	int	order,
		bool	forceTensorRule
	)

Definition at line 3346 of file GaussQuadratureTet.cpp.

Referenced by gaussIntegration::get(), MTetrahedron::getIntegrationPoints(), and gaussIntegration::getTetrahedron().

Here is the call graph for this function:

Here is the caller graph for this function:

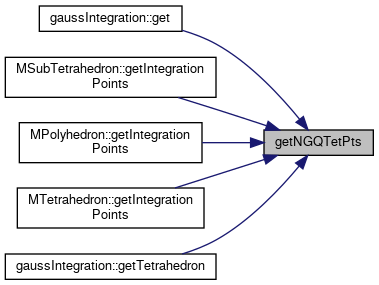
getNGQTetPts()

int getNGQTetPts	(	int	order,
		bool	forceTensorRule
	)

Definition at line 3362 of file GaussQuadratureTet.cpp.

Referenced by gaussIntegration::get(), MSubTetrahedron::getIntegrationPoints(), MPolyhedron::getIntegrationPoints(), MTetrahedron::getIntegrationPoints(), and gaussIntegration::getTetrahedron().

Here is the caller graph for this function:

GQTetGL()

static std::vector<IntPt *> GQTetGL ( 40  , nullptr    )

static

Referenced by getGQTetPts().

Here is the caller graph for this function:

Variable Documentation

GQTet

IntPt* GQTet[7] = {GQTet1, GQTet1, GQTet2, GQTet3, GQTet4, GQTet5, GQTet6}

Definition at line 92 of file GaussQuadratureTet.cpp.

GQTet1

IntPt GQTet1[1] = {{{.25, .25, .25}, 0.166666666666667}}

Definition at line 51 of file GaussQuadratureTet.cpp.

GQTet2

IntPt GQTet2[4]

Initial value:

= {{{a4, b4, b4}, 0.0416666666666667},
                   {{b4, a4, b4}, 0.0416666666666667},
                   {{b4, b4, a4}, 0.0416666666666667},
                   {{b4, b4, b4}, 0.0416666666666667}}

Definition at line 53 of file GaussQuadratureTet.cpp.

GQTet3

IntPt GQTet3[5]

Initial value:

= {{{0.25, 0.25, 0.25}, -0.133333333333333},
                   {{a5, b5, b5}, 0.075},
                   {{b5, a5, b5}, 0.075},
                   {{b5, b5, a5}, 0.075},
                   {{b5, b5, b5}, 0.075}}

Definition at line 58 of file GaussQuadratureTet.cpp.

GQTet4

IntPt GQTet4[16]

Initial value:

= {
  {{c16, d16, d16}, a16}, {{d16, c16, d16}, a16}, {{d16, d16, c16}, a16},
  {{d16, d16, d16}, a16}, {{e16, f16, g16}, b16}, {{f16, e16, g16}, b16},
  {{e16, g16, g16}, b16}, {{f16, g16, g16}, b16}, {{g16, g16, e16}, b16},
  {{g16, g16, f16}, b16}, {{g16, e16, f16}, b16}, {{g16, f16, e16}, b16},
  {{e16, g16, f16}, b16}, {{f16, g16, e16}, b16}, {{g16, e16, g16}, b16},
  {{g16, f16, g16}, b16}}

Definition at line 64 of file GaussQuadratureTet.cpp.

GQTet5

IntPt GQTet5[17]

Initial value:

= {
  {{0.25, 0.25, 0.25}, a17}, {{p17, q17, q17}, b17}, {{q17, p17, q17}, b17},
  {{q17, q17, p17}, b17},    {{q17, q17, q17}, b17}, {{e17, f17, g17}, c17},
  {{f17, e17, g17}, c17},    {{e17, g17, g17}, c17}, {{f17, g17, g17}, c17},
  {{g17, g17, e17}, c17},    {{g17, g17, f17}, c17}, {{g17, e17, f17}, c17},
  {{g17, f17, e17}, c17},    {{e17, g17, f17}, c17}, {{f17, g17, e17}, c17},
  {{g17, e17, g17}, c17},    {{g17, f17, g17}, c17}}

Definition at line 72 of file GaussQuadratureTet.cpp.

GQTet6

IntPt GQTet6[29]

Initial value:

= {
  {{0.25, 0.25, 0.25}, a29}, {{p29, q29, q29}, b29}, {{q29, p29, q29}, b29},
  {{q29, q29, p29}, b29},    {{q29, q29, q29}, b29}, {{e29, f29, g29}, c29},
  {{f29, e29, g29}, c29},    {{e29, g29, g29}, c29}, {{f29, g29, g29}, c29},
  {{g29, g29, e29}, c29},    {{g29, g29, f29}, c29}, {{g29, e29, f29}, c29},
  {{g29, f29, e29}, c29},    {{e29, g29, f29}, c29}, {{f29, g29, e29}, c29},
  {{g29, e29, g29}, c29},    {{g29, f29, g29}, c29}, {{h29, i29, j29}, d29},
  {{i29, h29, j29}, d29},    {{h29, j29, j29}, d29}, {{i29, j29, j29}, d29},
  {{j29, j29, h29}, d29},    {{j29, j29, i29}, d29}, {{j29, h29, i29}, d29},
  {{j29, i29, h29}, d29},    {{h29, j29, i29}, d29}, {{i29, j29, h29}, d29},
  {{j29, h29, j29}, d29},    {{j29, i29, j29}, d29}}

Definition at line 80 of file GaussQuadratureTet.cpp.

GQTetnPt

int GQTetnPt[7] = {1, 1, 4, 5, 16, 17, 29}

Definition at line 93 of file GaussQuadratureTet.cpp.

GQTetnPtSolin

int GQTetnPtSolin[22]

static

Initial value:

= {1,   1,   4,   5,   11,   14,  24,  31,
                                43,  53,  126, 126, 210,  210, 330, 330,
                                495, 495, 715, 715, 1001, 1001}

Definition at line 3341 of file GaussQuadratureTet.cpp.

Referenced by getNGQTetPts().

GQTetSolin

IntPt* GQTetSolin[22]

static

Initial value:

= {
  tetP1Solin,  tetP1Solin,  tetP2Solin,  tetP3Solin,  tetP4Solin,  tetP5Solin,
  tetP6Solin,  tetP7Solin,  tetP8Solin,  tetP9Solin,  tetP11Solin, tetP11Solin,
  tetP13Solin, tetP13Solin, tetP15Solin, tetP15Solin, tetP17Solin, tetP17Solin,
  tetP19Solin, tetP19Solin, tetP21Solin, tetP21Solin}

Definition at line 3336 of file GaussQuadratureTet.cpp.

Referenced by getGQTetPts().

tetP11Solin

IntPt tetP11Solin[126]

Quadrature rule for an interpolation of order 11 on the tetrahedron

Definition at line 415 of file GaussQuadratureTet.cpp.

tetP13Solin

IntPt tetP13Solin[210]

Quadrature rule for an interpolation of order 13 on the tetrahedron

Definition at line 549 of file GaussQuadratureTet.cpp.

tetP15Solin

IntPt tetP15Solin[330]

Quadrature rule for an interpolation of order 15 on the tetrahedron

Definition at line 767 of file GaussQuadratureTet.cpp.

tetP17Solin

IntPt tetP17Solin[495]

Quadrature rule for an interpolation of order 17 on the tetrahedron

Definition at line 1105 of file GaussQuadratureTet.cpp.

tetP19Solin

IntPt tetP19Solin[715]

Quadrature rule for an interpolation of order 19 on the tetrahedron

Definition at line 1608 of file GaussQuadratureTet.cpp.

tetP1Solin

IntPt tetP1Solin[1] = {{{0.25, 0.25, 0.25}, 0.166666666666667}}

Quadrature rule for an interpolation of order 1 on the tetrahedron

Definition at line 99 of file GaussQuadratureTet.cpp.

tetP21Solin

IntPt tetP21Solin[1001]

Quadrature rule for an interpolation of order 21 on the tetrahedron

Definition at line 2331 of file GaussQuadratureTet.cpp.

tetP2Solin

IntPt tetP2Solin[4]

Initial value:

= {
  {{0.138196601125, 0.138196601125, 0.138196601125}, 0.0416666666666667},
  {{0.585410196625, 0.138196601125, 0.138196601125}, 0.0416666666666667},
  {{0.138196601125, 0.585410196625, 0.138196601125}, 0.0416666666666667},
  {{0.138196601125, 0.138196601125, 0.585410196625}, 0.0416666666666667}}

Quadrature rule for an interpolation of order 2 on the tetrahedron

Definition at line 108 of file GaussQuadratureTet.cpp.

tetP3Solin

IntPt tetP3Solin[5]

Initial value:

= {
  {{0.250000000000, 0.250000000000, 0.250000000000}, -0.133333333333333},
  {{0.166666666667, 0.166666666667, 0.166666666667}, +0.075000000000000},
  {{0.166666666667, 0.166666666667, 0.500000000000}, +0.075000000000000},
  {{0.166666666667, 0.500000000000, 0.166666666667}, +0.075000000000000},
  {{0.500000000000, 0.166666666667, 0.166666666667}, +0.075000000000000}}

Quadrature rule for an interpolation of order 3 on the tetrahedron

Definition at line 121 of file GaussQuadratureTet.cpp.

tetP4Solin

IntPt tetP4Solin[11]

Initial value:

= {
  {{0.2500000000000, 0.2500000000000, 0.2500000000000}, -0.0131555555555},
  {{0.0714285714286, 0.0714285714286, 0.0714285714286}, +0.0076222222222},
  {{0.0714285714286, 0.0714285714286, 0.7857142857140}, +0.0076222222222},
  {{0.0714285714286, 0.7857142857140, 0.0714285714286}, +0.0076222222222},
  {{0.7857142857140, 0.0714285714286, 0.0714285714286}, +0.0076222222222},
  {{0.3994035761670, 0.3994035761670, 0.1005964238330}, +0.0248888888888},
  {{0.3994035761670, 0.1005964238330, 0.3994035761670}, +0.0248888888888},
  {{0.1005964238330, 0.3994035761670, 0.3994035761670}, +0.0248888888888},
  {{0.3994035761670, 0.1005964238330, 0.1005964238330}, +0.0248888888888},
  {{0.1005964238330, 0.3994035761670, 0.1005964238330}, +0.0248888888888},
  {{0.1005964238330, 0.1005964238330, 0.3994035761670}, +0.0248888888888}}

Quadrature rule for an interpolation of order 4 on the tetrahedron

Definition at line 135 of file GaussQuadratureTet.cpp.

tetP5Solin

IntPt tetP5Solin[14]

Initial value:

= {
  {{0.0927352503109, 0.0927352503109, 0.0927352503109}, 0.01224884051940},
  {{0.7217942490670, 0.0927352503109, 0.0927352503109}, 0.01224884051940},
  {{0.0927352503109, 0.7217942490670, 0.0927352503109}, 0.01224884051940},
  {{0.0927352503109, 0.0927352503109, 0.7217942490670}, 0.01224884051940},
  {{0.3108859192630, 0.3108859192630, 0.3108859192630}, 0.01878132095300},
  {{0.0673422422101, 0.3108859192630, 0.3108859192630}, 0.01878132095300},
  {{0.3108859192630, 0.0673422422101, 0.3108859192630}, 0.01878132095300},
  {{0.3108859192630, 0.3108859192630, 0.0673422422101}, 0.01878132095300},
  {{0.4544962958740, 0.4544962958740, 0.0455037041256}, 0.00709100346285},
  {{0.4544962958740, 0.0455037041256, 0.4544962958740}, 0.00709100346285},
  {{0.0455037041256, 0.4544962958740, 0.4544962958740}, 0.00709100346285},
  {{0.4544962958740, 0.0455037041256, 0.0455037041256}, 0.00709100346285},
  {{0.0455037041256, 0.4544962958740, 0.0455037041256}, 0.00709100346285},
  {{0.0455037041256, 0.0455037041256, 0.4544962958740}, 0.00709100346285}}

Quadrature rule for an interpolation of order 5 on the tetrahedron

Definition at line 155 of file GaussQuadratureTet.cpp.

tetP6Solin

IntPt tetP6Solin[24]

Initial value:

= {
  {{0.2146028712590, 0.2146028712590, 0.2146028712590}, 0.006653791709700},
  {{0.3561913862230, 0.2146028712590, 0.2146028712590}, 0.006653791709700},
  {{0.2146028712590, 0.3561913862230, 0.2146028712590}, 0.006653791709700},
  {{0.2146028712590, 0.2146028712590, 0.3561913862230}, 0.006653791709700},
  {{0.0406739585346, 0.0406739585346, 0.0406739585346}, 0.001679535175883},
  {{0.8779781243960, 0.0406739585346, 0.0406739585346}, 0.001679535175883},
  {{0.0406739585346, 0.8779781243960, 0.0406739585346}, 0.001679535175883},
  {{0.0406739585346, 0.0406739585346, 0.8779781243960}, 0.001679535175883},
  {{0.3223378901420, 0.3223378901420, 0.3223378901420}, 0.009226196923950},
  {{0.0329863295732, 0.3223378901420, 0.3223378901420}, 0.009226196923950},
  {{0.3223378901420, 0.0329863295732, 0.3223378901420}, 0.009226196923950},
  {{0.3223378901420, 0.3223378901420, 0.0329863295732}, 0.009226196923950},
  {{0.0636610018750, 0.0636610018750, 0.2696723314580}, 0.008035714285717},
  {{0.0636610018750, 0.2696723314580, 0.0636610018750}, 0.008035714285717},
  {{0.0636610018750, 0.0636610018750, 0.6030056647920}, 0.008035714285717},
  {{0.0636610018750, 0.6030056647920, 0.0636610018750}, 0.008035714285717},
  {{0.0636610018750, 0.2696723314580, 0.6030056647920}, 0.008035714285717},
  {{0.0636610018750, 0.6030056647920, 0.2696723314580}, 0.008035714285717},
  {{0.2696723314580, 0.0636610018750, 0.0636610018750}, 0.008035714285717},
  {{0.2696723314580, 0.0636610018750, 0.6030056647920}, 0.008035714285717},
  {{0.2696723314580, 0.6030056647920, 0.0636610018750}, 0.008035714285717},
  {{0.6030056647920, 0.0636610018750, 0.2696723314580}, 0.008035714285717},
  {{0.6030056647920, 0.0636610018750, 0.0636610018750}, 0.008035714285717},
  {{0.6030056647920, 0.2696723314580, 0.0636610018750}, 0.008035714285717}}

Quadrature rule for an interpolation of order 6 on the tetrahedron

Definition at line 178 of file GaussQuadratureTet.cpp.

tetP7Solin

IntPt tetP7Solin[31]

Quadrature rule for an interpolation of order 7 on the tetrahedron

Definition at line 211 of file GaussQuadratureTet.cpp.

tetP8Solin

IntPt tetP8Solin[43]

Quadrature rule for an interpolation of order 8 on the tetrahedron

Definition at line 250 of file GaussQuadratureTet.cpp.

tetP9Solin

IntPt tetP9Solin[53]

Quadrature rule for an interpolation of order 9 on the tetrahedron

Definition at line 301 of file GaussQuadratureTet.cpp.