#include <math.h>
#include <list>
#include <set>
#include <algorithm>
#include "adaptiveData.h"
#include "PViewDataGModel.h"
#include "Plugin.h"
#include "OS.h"
#include "GmshDefines.h"

Include dependency graph for adaptiveData.cpp:

Functions
template<class T >
static void	cleanElement ()

static void	computeShapeFunctions (fullMatrix< double > coeffs, fullMatrix< double > eexps, double u, double v, double w, fullVector< double > sf, fullVector< double > tmp)

static void	computeShapeFunctionsPyramid (fullMatrix< double > coeffs, fullMatrix< double > eexps, double u, double v, double w, fullVector< double > sf, fullVector< double > tmp)

Function Documentation

◆ cleanElement()

template<class T >

static void cleanElement ( )

static

Definition at line 59 of file adaptiveData.cpp.

◆ computeShapeFunctions()

static void computeShapeFunctions	(	fullMatrix< double > *	coeffs,
		fullMatrix< double > *	eexps,
		double	u,
		double	v,
		double	w,
		fullVector< double > *	sf,
		fullVector< double > *	tmp
	)

static

Definition at line 66 of file adaptiveData.cpp.

Referenced by adaptiveElements< T >::init().

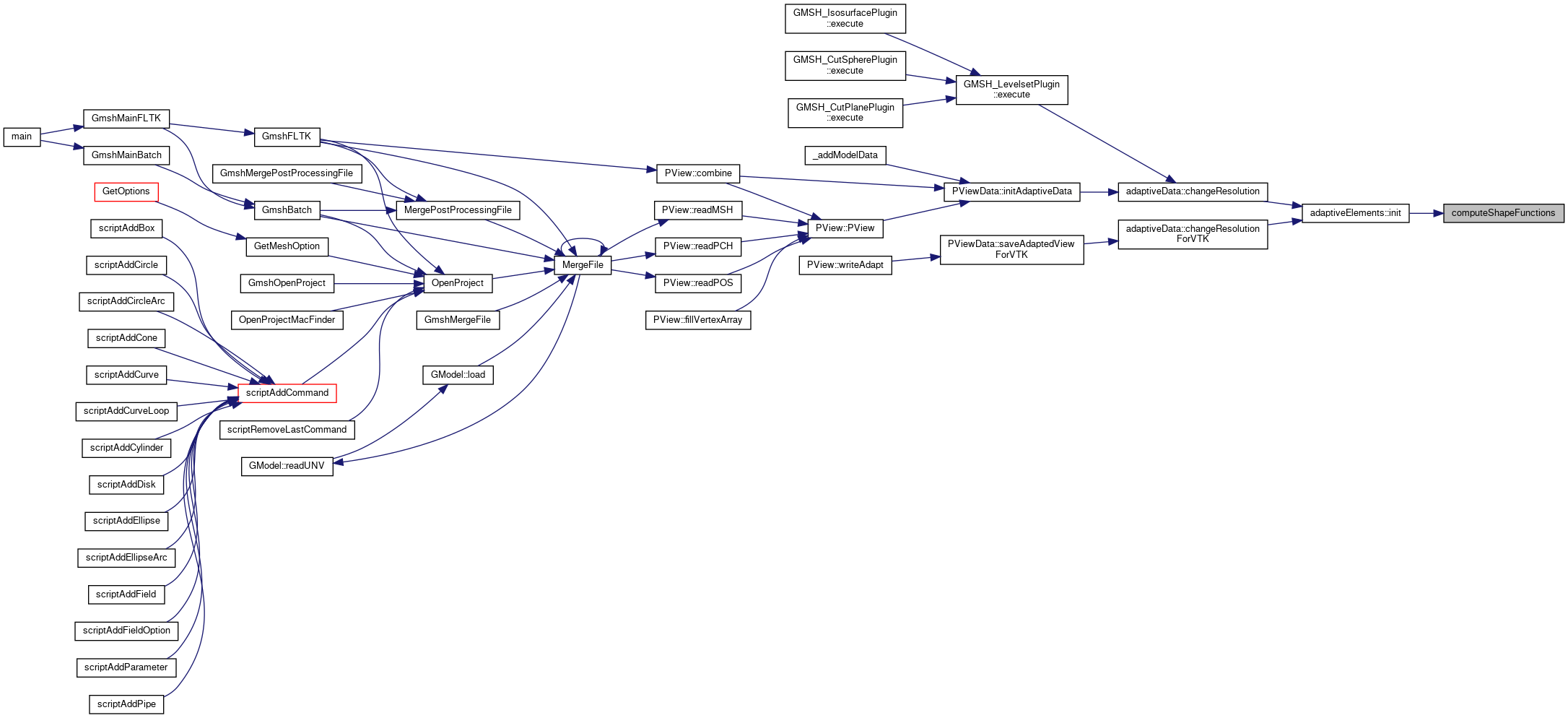
Here is the call graph for this function:

Here is the caller graph for this function:

◆ computeShapeFunctionsPyramid()

static void computeShapeFunctionsPyramid	(	fullMatrix< double > *	coeffs,
		fullMatrix< double > *	eexps,
		double	u,
		double	v,
		double	w,
		fullVector< double > *	sf,
		fullVector< double > *	tmp
	)

static

Bergot space is characterised by polynomials $\mathcal B_{ijk} = \mathcal P_i \left(\frac{\xi }{1-\zeta}\right) \mathcal P_j \left(\frac{\eta}{1-\zeta}\right) \left(1-\zeta\right)^{max(i,j)} \mathcal P^{2 max(i,j),0}_k \left(2 \zeta -1\right)~|~i,j \leq p, k \leq p - max(i,j)$ and hence by the "monomials" $\mu_{ijk} = \left(\frac{\xi }{1-\zeta}\right)^i \left(\frac{\eta}{1-\zeta}\right)^j \left(1-\zeta\right)^{max(i,j)} \zeta^k~|~i,j \leq p~,~k \leq p-max(i,j)$

Definition at line 90 of file adaptiveData.cpp.

Here is the call graph for this function: